Saturday, January 16, 2010
Sunday, January 10, 2010
The Heat Island Effect: Lost and Found
As I've demonstrated (to my own satisfaction, at least) the strange, arcane adjustments for HIE made by CRU and GISS are not even necessary. One gets the same trends whether they are made(GISS Data Set 2) or not (GISS Data Set 1) if an unbiased and well understood method for determining temperature anomalies is used. What exactly they are doing with those adjustments is up in the air, but the question remains to what extent the HIE is affecting the results that we are seeing for global temperatures.
Analysis of the GISS station data had begun to make me think that the heat island effect did not exist. But yesterday I was looking over station data from the local Houston area, and it did seem that there was an obvious HIE. Individual stations in the heart of the city, inside the loop, were reading about 3 or 4 degrees above those out in the suburbs and beyond. It was striking to me, though, how quickly the readings came back down to match those of the surrounding countryside getting even a little away from the city center.
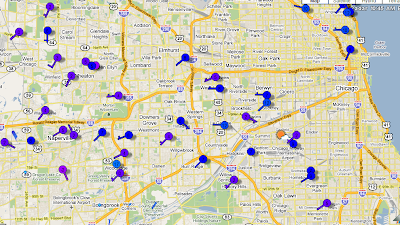
Looking at other cities I found the same thing. wunderderground.com enables one to look at dozens of individual stations in an area simultaneously. Note how in Chicago the temperature readings decline as one gets away from the city center:
And here is the New York City area:

Compare to the surrounding regions:

Note the two stations in the middle of Manhattan. They are located 500 feet up.
Unless stations were actually within the city they would not detect the effect.
So, looking back over the maps of GISS station locations, it hit me that the vast majority of those stations marked as urban are not urban at all, at least not to the extent that was seemingly needed to find a HIE. All this time the suspicion has been that the stations marked rural are too urbanized when it could be exactly the opposite. Those marked urban are often not that urban.
Thus, I selected stations from the 85 largest urban centers in the world. In order the qualify the station had to be within the urban area, urban sprawl for 0.1 degrees latitude or longitude in every direction from the designated station location (which is provided to the nearest tenth of a degree). The temperature anomalies for these, as determined by the statistical algorithm used in previous posts, is compared to the published GISS data below:

To make a long story short, as more cities are added in to the list of city stations included in the analysis above, from smaller and smaller cities, the trend line comes down to be much closer to that of the GISS data. And this is still well short, only about 10%, of the stations listed as urban in the giss.dset1 data. As I've shown previously, if all the "urban" stations are included the HIE disappears.
Analysis of the GISS station data had begun to make me think that the heat island effect did not exist. But yesterday I was looking over station data from the local Houston area, and it did seem that there was an obvious HIE. Individual stations in the heart of the city, inside the loop, were reading about 3 or 4 degrees above those out in the suburbs and beyond. It was striking to me, though, how quickly the readings came back down to match those of the surrounding countryside getting even a little away from the city center.
Looking at other cities I found the same thing. wunderderground.com enables one to look at dozens of individual stations in an area simultaneously. Note how in Chicago the temperature readings decline as one gets away from the city center:
And here is the New York City area:
Compare to the surrounding regions:
Note the two stations in the middle of Manhattan. They are located 500 feet up.
Unless stations were actually within the city they would not detect the effect.
So, looking back over the maps of GISS station locations, it hit me that the vast majority of those stations marked as urban are not urban at all, at least not to the extent that was seemingly needed to find a HIE. All this time the suspicion has been that the stations marked rural are too urbanized when it could be exactly the opposite. Those marked urban are often not that urban.
Thus, I selected stations from the 85 largest urban centers in the world. In order the qualify the station had to be within the urban area, urban sprawl for 0.1 degrees latitude or longitude in every direction from the designated station location (which is provided to the nearest tenth of a degree). The temperature anomalies for these, as determined by the statistical algorithm used in previous posts, is compared to the published GISS data below:

To make a long story short, as more cities are added in to the list of city stations included in the analysis above, from smaller and smaller cities, the trend line comes down to be much closer to that of the GISS data. And this is still well short, only about 10%, of the stations listed as urban in the giss.dset1 data. As I've shown previously, if all the "urban" stations are included the HIE disappears.
Saturday, January 09, 2010
Population Density and Global Warming
It has often been observed that the center of a city is warmer than the surrounding countryside. Thus the claim has been made that global warming is an error due to weather stations gradually being taken over by urbanization. As detailed in previous posts, I've been unable to demonstrate that from the weather station data available from NASA.
The hypothesis I address on this occasion is that idea that population density in a country could be used as a proxy of urbanization. If so, then there should be a correlation between population density change over time and the temperature in that region.
I used population density figures from the CIA World Fact Book and assumed an exponential decline in density from that time depending on time:
D = d*((100-g)/100)*exp((year-2008)/127)
where D = population density in a given year
d is the population density in 2008
g is the %growth in population in 2008
year is the year of measurement.
Thus D decreases in a log linear fashion over time proportional to the rate of growth observed in 2008, an attempt to mimick population growth.
Plugging this group into the random effects statistical algorithm used in previous posts, I found no relationship between D and temperature in 60 randomly selected countries:
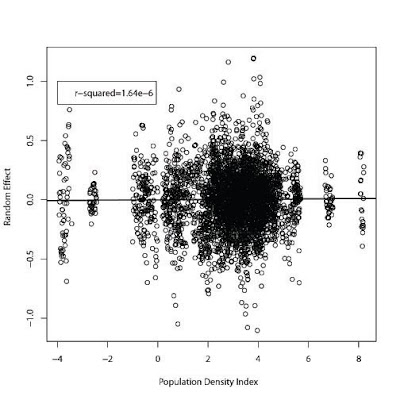
The x axis is the log of D (population density) and the y axis is degrees C.
No effect of population density over time emerges with this analysis.
The hypothesis I address on this occasion is that idea that population density in a country could be used as a proxy of urbanization. If so, then there should be a correlation between population density change over time and the temperature in that region.
I used population density figures from the CIA World Fact Book and assumed an exponential decline in density from that time depending on time:
D = d*((100-g)/100)*exp((year-2008)/127)
where D = population density in a given year
d is the population density in 2008
g is the %growth in population in 2008
year is the year of measurement.
Thus D decreases in a log linear fashion over time proportional to the rate of growth observed in 2008, an attempt to mimick population growth.
Plugging this group into the random effects statistical algorithm used in previous posts, I found no relationship between D and temperature in 60 randomly selected countries:

The x axis is the log of D (population density) and the y axis is degrees C.
No effect of population density over time emerges with this analysis.
Friday, January 08, 2010
Seeking A Heat Island Effect
Continuing on with the data mining of the GISSTEMP material, I have been looking for evidence of a heat island effect, and my conclusion is that it won't be found in this data.
Since my own analysis didn't show a robust HIE, I looked for bias in the dset1 data.
I thought it might be due to urban records being longer than rural ones and therefore dominating the data set. This did not prove out. The average length of rural and urban records is about the same.
I thought it might be inaccurate rural, suburban, and urban designations. But a review of 300 rural sites selected at random did not reveal a single obvious misclassification.
No matter how I parsed and combed through this data I was getting no significant difference in rural and urban stations. The best I've done is to see a 1.8 degree difference in the aggregate analysis that I've posted previously, and that does not necessarily represent a trend.
So, what are the possible explanations?
Here is my list of guesses:
1) The database is contaminated with thermometers that are sitting on asphalt or next to air conditioner compressors that are purported to be in rural locations.
2) The population density in the areas of the USA where most of the thermometers are located (the Northeast) has been flat or declining since 1950. Therefore, a grouping of U, R, or S or brightness in one cross-section in the database does not adequately represent the situation.
I don't have lot of enthusiasm for working through this possibility. It seems to me that even if the U, R, and S designations in the GISS data had errors that there would still be some differences emerging.
For what it's worth, here are the results of comparing locations that are designated rural and are not designated as airport locations versus all the rest of the locations using the random effects statistical algorithm described in previous posts:
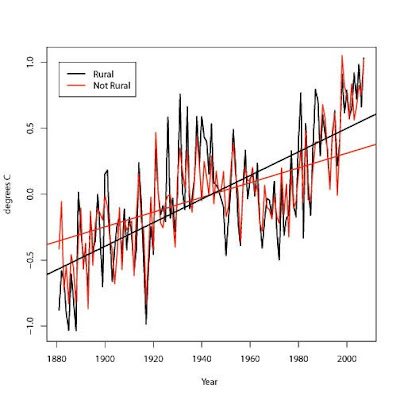
These are not the results I hoped for. But hiding them would make me no better than a climate scientist.
Since my own analysis didn't show a robust HIE, I looked for bias in the dset1 data.
I thought it might be due to urban records being longer than rural ones and therefore dominating the data set. This did not prove out. The average length of rural and urban records is about the same.
I thought it might be inaccurate rural, suburban, and urban designations. But a review of 300 rural sites selected at random did not reveal a single obvious misclassification.
No matter how I parsed and combed through this data I was getting no significant difference in rural and urban stations. The best I've done is to see a 1.8 degree difference in the aggregate analysis that I've posted previously, and that does not necessarily represent a trend.
So, what are the possible explanations?
Here is my list of guesses:
1) The database is contaminated with thermometers that are sitting on asphalt or next to air conditioner compressors that are purported to be in rural locations.
2) The population density in the areas of the USA where most of the thermometers are located (the Northeast) has been flat or declining since 1950. Therefore, a grouping of U, R, or S or brightness in one cross-section in the database does not adequately represent the situation.
I don't have lot of enthusiasm for working through this possibility. It seems to me that even if the U, R, and S designations in the GISS data had errors that there would still be some differences emerging.
For what it's worth, here are the results of comparing locations that are designated rural and are not designated as airport locations versus all the rest of the locations using the random effects statistical algorithm described in previous posts:

These are not the results I hoped for. But hiding them would make me no better than a climate scientist.
Wednesday, January 06, 2010
Tuesday, January 05, 2010
Climate Science
As Steve McIntyre has so brilliantly shown, Jim Hansen's methods for processing station temperatures into global temperatures don't really make sense.
The burning question for me therefore has been: If the stick guys' methods don't make sense and perhaps introduce bias, then what do we get when proper methods are used? What, exactly, is the truth of the matter?
And so I've worked through Steve's postings and the writings of others trying to find out what a proper method might be.
In a post from 18 months ago, Steve pointed out that the job of processing this data and eliminating the effects of various factors to come up with an estimation of the temperature anomalies over time could be done using well understood mixed effects statistical modeling algorithms. I thought it rather astounding that a statistical method seemingly completely different from Hansen's methods would come up with much the same results. Steve used this in modeling the combination of location data into grid cells, but why not apply it to the whole data set?
And so I tried that.
giss.dset0, you may recall is temperature data taken from different weather stations. In some cases these stations are all together in one location, as in 4 or 5 stations in a given city area. Hansen first combined these stations together for a location, then he did a lot of complicated smoothing and adjustment of the data in a series of steps. dset0 is raw data, dset1 includes some adjustments and combination of data of stations at given locations, dset2 includes more adjustments within a given location, and gridding of the data does more of the same, smoothing data over geometrical areas, between locations. With all of the adjusting and smoothing going on the introduction of some sort of bias seems likely. For example, Hansen always used the longest records to start with and then increased or decreased the shorter records to match the longer. But aren't the longer records usually from urban stations? Would this not cement the heat island effect into the combined location data?
And so, working in the R Project statistical package and following McIntyre's lead, I first reorganized the data in giss.dset0 into a simple long data frame with location information folded in from giss.info.
extr = function(giss.dset0, giss.info) {
year = 0; temp = 0; alt=0; ur=0; loc=0; lxs=0; sta=0
Ni = (1:length(giss.dset0))[!is.na(giss.dset0)]
for(i in Ni) #if(sum(is.na(giss.dset0[[i]])) > 0) next else
for(j in 1:length(giss.dset0[[i]])) if(is.na(giss.dset0[[i]][[j]])) next else
{
N = length(giss.dset0[[i]][[j]][[1]])
sta = c(sta, rep(names(giss.dset0[[i]])[j],N))
year = c(year, giss.dset0[[i]][[j]][[1]])
temp = c(temp, giss.dset0[[i]][[j]][[18]])
ur = c(ur, rep(giss.info$urban[i],N))
alt = c(alt, rep(250*(giss.info$alt.interp[i]%/%250),N))
tmp=substr(names(giss.dset0[[i]])[j],1,8)
loc = c(loc, rep(tmp, N))
lxs = c(lxs, rep(paste(tmp, "i", names(giss.dset0[[i]])[j],sep=""),N))
}
sta=sta[-1]; year=year[-1]; temp=temp[-1]; alt=alt[-1]; loc=loc[-1]
ur = ur[-1]; lxs=lxs[-1]
return(data.frame(loc=loc,sta=sta,year=year,ur=ur,alt=alt,lxs=lxs,temp=temp))
}
dset0.t = extr(giss.dset0, giss.info)
(No, I could not use monthly data without running out of memory.)
Then calculate random effects:
(load the lme4 package)
dset0.fm = lmer(temp~(1|loc)+(1|sta)+(1|ur)+(1|alt)+(1|year), data=dset0.t)
dset0.fm1 = lmer(temp~(1|sta)+(1|year), data=dset0.t)
(loc = location id, sta=station id with location, ur=urban vs suburban vs rural, alt= location altitude in 250 meter bands)
ranef(dset0.fm)$year and ranef(dset0.fm1)$year contain the random effects year over year. The temperature anomaly for each year, in other words. Most of the variance is dumped into other groups. Using more groupings in the model formula makes no difference in these estimates (dset0.fm vs dset0.fm1 R-squared = 0.999).
Here is your heat island effect:
> ranef(dset0.fm)$ur
(Intercept)
R -0.23716400 (rural)
S -0.04312743 (suburban)
U 0.28028908 (urban)
And here is the effect of altitude:
> ranef(dset0.fm)$alt
(Intercept)
0 10.0821297
250 9.5952519
500 8.2160810
750 7.4049196
1000 6.4774994
1250 5.4415439
1500 4.2931860
1750 3.4352673
2000 1.7974976
2250 -0.5588156
2500 -1.6522236
2750 -5.5811832
3000 -5.2383055
3250 -13.6373919
3500 -8.7024097
3750 -13.8671371
4000 1.2833311
4250 -6.0728011
4500 -3.3266110
4750 0.8495323
5000 -1.0044707
5750 -0.4843320
What that yearly random effect looks like compared to the GISSTEMP book numbers:

And here is the difference between the two:

R-squared = 0.73. Close enough for government work. The slope coefficients are nearly identical (a 0.00035 per year difference). And I'm sure that a statistician would do much better. Much of what Hansen did in step 1 and 2 and in gridding the data was smoothing. Application of a smoothing algorithm would no doubt take out the variation in the random effects estimation I got, but that would not improve the fidelity of the results.
dset0 annual averages are as close to the raw data as I can get without running out of computer memory. I went from that data to a final result with one command in R.
If I can come up with the same results with no spacial factors at all other than altitude and station grouping then does gridding mean anything? Can the analysis represent anything more than the 25% of the earth's surface the stations occupy?
Hansen is vindicated in a big respect. This shows that his methods, regardless how byzantine, introduce no significant amount of bias where temperature trends are concerned with regard to the station data available. The proof is in the pudding, and all that.
That lack of coverage of the earth's surface in station data, I'm guessing, is the reason for the difference in satellite, radiosonde, and station estimates of global temperature.
The amount of memory and processing power I have in my cheap, clearance priced desktop PC would have been duplicated by a computer the size of a city block, if at all, back in the days Hansen started doing this climate business. His multi step process of analyzing station data was perhaps an effort to perform an analysis that would have been impossible using the statistical methods I used here.
Update
Including another grouping factor, latitude in 5 degree bands, has no effect on the temperature anomalies, but it's interesting to look at the random effect for that group:
dset0.fm2 = lmer(temp~(1|ur)+(1|lat)+(1|alt)+(1|sta)+(1|year),
data=dset0.t)
> ranef(dset0.fm2)$lat
(Intercept)
-90 -48.0765255
-85 -30.6208086
-80 -30.5843329
-75 -26.8087508
-70 -17.5837928
-65 -10.6445832
-55 -0.4677458
-50 1.9302840
-45 4.6332613
-40 7.5261542
-35 10.1896612
-30 7.2221295
-25 16.5283583
-20 17.4532507
-15 18.3289638
-10 18.4701555
-5 18.5784181
0 18.7600821
5 19.5108772
10 19.8686941
15 19.7051168
20 17.5278219
25 15.0410194
30 11.2047241
35 7.3644670
40 3.2930061
45 -0.4509212
50 -0.3098546
55 -5.3064547
60 -9.0101544
65 -13.3917199
70 -16.3916299
75 -20.7265894
80 -22.7631131
And including that group gives more consistent altitude and urban estimates:
> ranef(dset0.fm2)$alt
(Intercept)
-1000 7.6009074
0 8.7884377
250 8.2316191
500 5.1136268
750 9.5794809
1000 5.9054092
1250 5.3426933
1500 4.0768528
1750 3.4410112
2000 2.0043036
2250 1.0247369
2500 -0.5251244
2750 -1.8542720
3000 -0.6135464
3250 -8.0035847
3500 -3.3222669
3750 -5.1468110
4000 -5.1510483
4250 -8.3572983
4500 -8.9318326
4750 -5.5925205
5000 -5.9627467
5750 -7.6483137
> ranef(dset0.fm2)$ur
(Intercept)
R -0.89551186
S -0.03941906
U 0.93493366
Here is the summary from lmer():
Linear mixed model fit by REML
Formula: temp ~ (1 | loc) + (1 | sta) + (1 | ur) + (1 | alt) + (1 | year)
Data: dset0.t
AIC BIC logLik deviance REMLdev
1274202 1274280 -637094 1274190 1274188
Random effects:
Groups Name Variance Std.Dev.
sta (Intercept) 0.510624 0.71458
loc (Intercept) 113.129532 10.63624
year (Intercept) 0.141931 0.37674
alt (Intercept) 29.856394 5.46410
ur (Intercept) 0.068179 0.26111
Residual 0.521113 0.72188
Number of obs: 548500, groups: sta, 13483; loc, 4514; year, 127; alt, 23; ur, 3
Fixed effects:
Estimate Std. Error t value
(Intercept) 5.20 1.25 4.159
Linear mixed model fit by REML
Formula: temp ~ (1 | ur) + (1 | lat) + (1 | alt) + (1 | sta) + (1 | year)
Data: dset0.t
AIC BIC logLik deviance REMLdev
1288347 1288426 -644167 1288337 1288333
Random effects:
Groups Name Variance Std.Dev.
sta (Intercept) 11.67732 3.41721
year (Intercept) 0.14162 0.37633
lat (Intercept) 330.71739 18.18564
alt (Intercept) 38.58698 6.21184
ur (Intercept) 0.84184 0.91752
Residual 0.52133 0.72203
Number of obs: 548500, groups: sta, 13483; year, 127; lat, 34; alt, 23; ur, 3
Fixed effects:
Estimate Std. Error t value
(Intercept) -1.544 3.427 -0.451
Update II
I get almost exactly the same results with the model used in the first update when I do the analysis with giss.dset2 (R-squared of temp random effects = 0.97)
The burning question for me therefore has been: If the stick guys' methods don't make sense and perhaps introduce bias, then what do we get when proper methods are used? What, exactly, is the truth of the matter?
And so I've worked through Steve's postings and the writings of others trying to find out what a proper method might be.
In a post from 18 months ago, Steve pointed out that the job of processing this data and eliminating the effects of various factors to come up with an estimation of the temperature anomalies over time could be done using well understood mixed effects statistical modeling algorithms. I thought it rather astounding that a statistical method seemingly completely different from Hansen's methods would come up with much the same results. Steve used this in modeling the combination of location data into grid cells, but why not apply it to the whole data set?
And so I tried that.
giss.dset0, you may recall is temperature data taken from different weather stations. In some cases these stations are all together in one location, as in 4 or 5 stations in a given city area. Hansen first combined these stations together for a location, then he did a lot of complicated smoothing and adjustment of the data in a series of steps. dset0 is raw data, dset1 includes some adjustments and combination of data of stations at given locations, dset2 includes more adjustments within a given location, and gridding of the data does more of the same, smoothing data over geometrical areas, between locations. With all of the adjusting and smoothing going on the introduction of some sort of bias seems likely. For example, Hansen always used the longest records to start with and then increased or decreased the shorter records to match the longer. But aren't the longer records usually from urban stations? Would this not cement the heat island effect into the combined location data?
And so, working in the R Project statistical package and following McIntyre's lead, I first reorganized the data in giss.dset0 into a simple long data frame with location information folded in from giss.info.
extr = function(giss.dset0, giss.info) {
year = 0; temp = 0; alt=0; ur=0; loc=0; lxs=0; sta=0
Ni = (1:length(giss.dset0))[!is.na(giss.dset0)]
for(i in Ni) #if(sum(is.na(giss.dset0[[i]])) > 0) next else
for(j in 1:length(giss.dset0[[i]])) if(is.na(giss.dset0[[i]][[j]])) next else
{
N = length(giss.dset0[[i]][[j]][[1]])
sta = c(sta, rep(names(giss.dset0[[i]])[j],N))
year = c(year, giss.dset0[[i]][[j]][[1]])
temp = c(temp, giss.dset0[[i]][[j]][[18]])
ur = c(ur, rep(giss.info$urban[i],N))
alt = c(alt, rep(250*(giss.info$alt.interp[i]%/%250),N))
tmp=substr(names(giss.dset0[[i]])[j],1,8)
loc = c(loc, rep(tmp, N))
lxs = c(lxs, rep(paste(tmp, "i", names(giss.dset0[[i]])[j],sep=""),N))
}
sta=sta[-1]; year=year[-1]; temp=temp[-1]; alt=alt[-1]; loc=loc[-1]
ur = ur[-1]; lxs=lxs[-1]
return(data.frame(loc=loc,sta=sta,year=year,ur=ur,alt=alt,lxs=lxs,temp=temp))
}
dset0.t = extr(giss.dset0, giss.info)
(No, I could not use monthly data without running out of memory.)
Then calculate random effects:
(load the lme4 package)
dset0.fm = lmer(temp~(1|loc)+(1|sta)+(1|ur)+(1|alt)+(1|year), data=dset0.t)
dset0.fm1 = lmer(temp~(1|sta)+(1|year), data=dset0.t)
(loc = location id, sta=station id with location, ur=urban vs suburban vs rural, alt= location altitude in 250 meter bands)
ranef(dset0.fm)$year and ranef(dset0.fm1)$year contain the random effects year over year. The temperature anomaly for each year, in other words. Most of the variance is dumped into other groups. Using more groupings in the model formula makes no difference in these estimates (dset0.fm vs dset0.fm1 R-squared = 0.999).
Here is your heat island effect:
> ranef(dset0.fm)$ur
(Intercept)
R -0.23716400 (rural)
S -0.04312743 (suburban)
U 0.28028908 (urban)
And here is the effect of altitude:
> ranef(dset0.fm)$alt
(Intercept)
0 10.0821297
250 9.5952519
500 8.2160810
750 7.4049196
1000 6.4774994
1250 5.4415439
1500 4.2931860
1750 3.4352673
2000 1.7974976
2250 -0.5588156
2500 -1.6522236
2750 -5.5811832
3000 -5.2383055
3250 -13.6373919
3500 -8.7024097
3750 -13.8671371
4000 1.2833311
4250 -6.0728011
4500 -3.3266110
4750 0.8495323
5000 -1.0044707
5750 -0.4843320
What that yearly random effect looks like compared to the GISSTEMP book numbers:

And here is the difference between the two:

R-squared = 0.73. Close enough for government work. The slope coefficients are nearly identical (a 0.00035 per year difference). And I'm sure that a statistician would do much better. Much of what Hansen did in step 1 and 2 and in gridding the data was smoothing. Application of a smoothing algorithm would no doubt take out the variation in the random effects estimation I got, but that would not improve the fidelity of the results.
dset0 annual averages are as close to the raw data as I can get without running out of computer memory. I went from that data to a final result with one command in R.
If I can come up with the same results with no spacial factors at all other than altitude and station grouping then does gridding mean anything? Can the analysis represent anything more than the 25% of the earth's surface the stations occupy?
Hansen is vindicated in a big respect. This shows that his methods, regardless how byzantine, introduce no significant amount of bias where temperature trends are concerned with regard to the station data available. The proof is in the pudding, and all that.
That lack of coverage of the earth's surface in station data, I'm guessing, is the reason for the difference in satellite, radiosonde, and station estimates of global temperature.
The amount of memory and processing power I have in my cheap, clearance priced desktop PC would have been duplicated by a computer the size of a city block, if at all, back in the days Hansen started doing this climate business. His multi step process of analyzing station data was perhaps an effort to perform an analysis that would have been impossible using the statistical methods I used here.
Update
Including another grouping factor, latitude in 5 degree bands, has no effect on the temperature anomalies, but it's interesting to look at the random effect for that group:
dset0.fm2 = lmer(temp~(1|ur)+(1|lat)+(1|alt)+(1|sta)+(1|year),
data=dset0.t)
> ranef(dset0.fm2)$lat
(Intercept)
-90 -48.0765255
-85 -30.6208086
-80 -30.5843329
-75 -26.8087508
-70 -17.5837928
-65 -10.6445832
-55 -0.4677458
-50 1.9302840
-45 4.6332613
-40 7.5261542
-35 10.1896612
-30 7.2221295
-25 16.5283583
-20 17.4532507
-15 18.3289638
-10 18.4701555
-5 18.5784181
0 18.7600821
5 19.5108772
10 19.8686941
15 19.7051168
20 17.5278219
25 15.0410194
30 11.2047241
35 7.3644670
40 3.2930061
45 -0.4509212
50 -0.3098546
55 -5.3064547
60 -9.0101544
65 -13.3917199
70 -16.3916299
75 -20.7265894
80 -22.7631131
And including that group gives more consistent altitude and urban estimates:
> ranef(dset0.fm2)$alt
(Intercept)
-1000 7.6009074
0 8.7884377
250 8.2316191
500 5.1136268
750 9.5794809
1000 5.9054092
1250 5.3426933
1500 4.0768528
1750 3.4410112
2000 2.0043036
2250 1.0247369
2500 -0.5251244
2750 -1.8542720
3000 -0.6135464
3250 -8.0035847
3500 -3.3222669
3750 -5.1468110
4000 -5.1510483
4250 -8.3572983
4500 -8.9318326
4750 -5.5925205
5000 -5.9627467
5750 -7.6483137
> ranef(dset0.fm2)$ur
(Intercept)
R -0.89551186
S -0.03941906
U 0.93493366
Here is the summary from lmer():
Linear mixed model fit by REML
Formula: temp ~ (1 | loc) + (1 | sta) + (1 | ur) + (1 | alt) + (1 | year)
Data: dset0.t
AIC BIC logLik deviance REMLdev
1274202 1274280 -637094 1274190 1274188
Random effects:
Groups Name Variance Std.Dev.
sta (Intercept) 0.510624 0.71458
loc (Intercept) 113.129532 10.63624
year (Intercept) 0.141931 0.37674
alt (Intercept) 29.856394 5.46410
ur (Intercept) 0.068179 0.26111
Residual 0.521113 0.72188
Number of obs: 548500, groups: sta, 13483; loc, 4514; year, 127; alt, 23; ur, 3
Fixed effects:
Estimate Std. Error t value
(Intercept) 5.20 1.25 4.159
Linear mixed model fit by REML
Formula: temp ~ (1 | ur) + (1 | lat) + (1 | alt) + (1 | sta) + (1 | year)
Data: dset0.t
AIC BIC logLik deviance REMLdev
1288347 1288426 -644167 1288337 1288333
Random effects:
Groups Name Variance Std.Dev.
sta (Intercept) 11.67732 3.41721
year (Intercept) 0.14162 0.37633
lat (Intercept) 330.71739 18.18564
alt (Intercept) 38.58698 6.21184
ur (Intercept) 0.84184 0.91752
Residual 0.52133 0.72203
Number of obs: 548500, groups: sta, 13483; year, 127; lat, 34; alt, 23; ur, 3
Fixed effects:
Estimate Std. Error t value
(Intercept) -1.544 3.427 -0.451
Update II
I get almost exactly the same results with the model used in the first update when I do the analysis with giss.dset2 (R-squared of temp random effects = 0.97)
Sunday, January 03, 2010
Climate Sciencapades IV
Someone told me back during the days when I took the anthropogenic global warming claims at face value that if I wanted to completely lose faith in the climate models I should take a look at them. And so I did, and he was right.
I looked at the code for the model used by GISS to do the predictions for the IPCC report of 2001. What is striking is how crude the model is. It divides the earth into a grid with about 8000 squares. The continental US is therefore represented by a 16 by 36 grid. Then there is what is not in the model. There's no way to model clouds and rain, so they have to make a guess at what those will be doing in response to changes in other factors. Consider that a 2% change in average cloud cover would completely negate any warming due to CO2 doubling. And the natural variability of cloud cover year to year and decade to decade is much larger than 2 percent.
The assumption of the modelers has been that a slight increase in temperature due to CO2 would be magnified by the resulting increase in water vapor in the air. But that might also result in an increase in cloud formation, which would offset the water vapor feedback.
Satellite measurements of clouds, water vapor, and temperature in the tropics show cycles. Heat forcing increases, temperatures increase, water vapor increases, and then clouds increase resulting, apparently, in a fall in temps. Rinse and repeat.
And the distribution of water vapor in the atmosphere is not uniform. Even over the open oceans the humidity is less than 100% most of the time, and it varies constantly in response to other factors. Satellite pictures of water vapor show that it swirls around in a more or less random fashion in the atmosphere. And CO2 does the same thing. Simple assumptions about these things won't do. And the models have a host of other fudge factors that can be tweaked endlessly until the model coughs up the desired results. The agreement between various modelers is not evidence of the validity of the results.
In any case, I have no faith in the computer models, having seen how they work.
More recently I became interested in surface temperature measurements, as reflected in previous posts. I wanted to know why satellite measurements of global temperatures don't agree with surface measurements. And so I looked at the data from GISS. I didn't appreciate the problem until I started trying to come up with a global average from station measurements. And then I found that the stations only represent about 25% of the earth's surface. I don't care how clever you are with statistics, there is no way in hell that you can come up with an accurate measurement of global temperatures if you're not even looking at three fourths of the globe, and that's really all I need to explain the difference between surface and satellite results. Trends can be determined by using a limited set of measurements, but as one area goes up another might be going down, as we have often found is the case.
Therefore, the four alarm increases in temperatures, according to GISS, NOAA, and others, over the last 30 years are probably not valid. Much closer to accurate is the satellite data, which shows a much more sedate rate of increase on the order of 0.14 degrees C per decade since 1972. The disagreement between satellite and temperature data has given rise to efforts to reconcile the two mainly by "adjusting" the satellite data using computer models(!) among other things. Which is doing it exactly the wrong way around.
I looked at the code for the model used by GISS to do the predictions for the IPCC report of 2001. What is striking is how crude the model is. It divides the earth into a grid with about 8000 squares. The continental US is therefore represented by a 16 by 36 grid. Then there is what is not in the model. There's no way to model clouds and rain, so they have to make a guess at what those will be doing in response to changes in other factors. Consider that a 2% change in average cloud cover would completely negate any warming due to CO2 doubling. And the natural variability of cloud cover year to year and decade to decade is much larger than 2 percent.
The assumption of the modelers has been that a slight increase in temperature due to CO2 would be magnified by the resulting increase in water vapor in the air. But that might also result in an increase in cloud formation, which would offset the water vapor feedback.
Satellite measurements of clouds, water vapor, and temperature in the tropics show cycles. Heat forcing increases, temperatures increase, water vapor increases, and then clouds increase resulting, apparently, in a fall in temps. Rinse and repeat.
And the distribution of water vapor in the atmosphere is not uniform. Even over the open oceans the humidity is less than 100% most of the time, and it varies constantly in response to other factors. Satellite pictures of water vapor show that it swirls around in a more or less random fashion in the atmosphere. And CO2 does the same thing. Simple assumptions about these things won't do. And the models have a host of other fudge factors that can be tweaked endlessly until the model coughs up the desired results. The agreement between various modelers is not evidence of the validity of the results.
In any case, I have no faith in the computer models, having seen how they work.
More recently I became interested in surface temperature measurements, as reflected in previous posts. I wanted to know why satellite measurements of global temperatures don't agree with surface measurements. And so I looked at the data from GISS. I didn't appreciate the problem until I started trying to come up with a global average from station measurements. And then I found that the stations only represent about 25% of the earth's surface. I don't care how clever you are with statistics, there is no way in hell that you can come up with an accurate measurement of global temperatures if you're not even looking at three fourths of the globe, and that's really all I need to explain the difference between surface and satellite results. Trends can be determined by using a limited set of measurements, but as one area goes up another might be going down, as we have often found is the case.
Therefore, the four alarm increases in temperatures, according to GISS, NOAA, and others, over the last 30 years are probably not valid. Much closer to accurate is the satellite data, which shows a much more sedate rate of increase on the order of 0.14 degrees C per decade since 1972. The disagreement between satellite and temperature data has given rise to efforts to reconcile the two mainly by "adjusting" the satellite data using computer models(!) among other things. Which is doing it exactly the wrong way around.
Saturday, January 02, 2010
Climate Sciencapades III
My interest in this material isn't in terms of trying to see if Hansen and the other stick players are doing things right. I'm more interested in seeing if processing the data in a simple and straightforward manner that makes sense to me gets results similar to what they are getting.
I've always had a great deal of trouble with the idea that a basic measurement like temperature is in need of massive computerized analysis. The temperature is the temperature, and it ought to be clear what's going on just by looking at the raw data, or something close to it.
So far we've seen that the differences between Hansen's dset0 and dset1 (raw and locally adjusted data respectively) are minimal when anomalies are calculated for each station or location. How about if the absolute temperatures are calculated?
So, I did this by averaging readings from the stations from dset0 in a given location together and then averaging all the locations from dset0 and then dset1 across years and then plotted the means to compare the two sets.

How much of the adjustment of dset0 is necessary if the two sets are so similar at the end of the adjustment process? Why build a gnarly black box of an analysis method if a simple and straightforward approach will do as well? When comparing dset0 and dset1 on a location by location basis the differences look pretty big in some cases, but apparently they don't make much difference overall. Perhaps adjustments are cancelling each other out.
Note that the plots look quite different from the plots of anomalies. The calculation of anomalies smooths the data considerably. This happens apparently because differences in locations are removed and many of the locations are not represented through the whole time period examined. The process of dealing with these difficulties is apparently handled by gridding the data, and for that I'll be looking into what McIntyre has found again.
I've always had a great deal of trouble with the idea that a basic measurement like temperature is in need of massive computerized analysis. The temperature is the temperature, and it ought to be clear what's going on just by looking at the raw data, or something close to it.
So far we've seen that the differences between Hansen's dset0 and dset1 (raw and locally adjusted data respectively) are minimal when anomalies are calculated for each station or location. How about if the absolute temperatures are calculated?
So, I did this by averaging readings from the stations from dset0 in a given location together and then averaging all the locations from dset0 and then dset1 across years and then plotted the means to compare the two sets.

How much of the adjustment of dset0 is necessary if the two sets are so similar at the end of the adjustment process? Why build a gnarly black box of an analysis method if a simple and straightforward approach will do as well? When comparing dset0 and dset1 on a location by location basis the differences look pretty big in some cases, but apparently they don't make much difference overall. Perhaps adjustments are cancelling each other out.
Note that the plots look quite different from the plots of anomalies. The calculation of anomalies smooths the data considerably. This happens apparently because differences in locations are removed and many of the locations are not represented through the whole time period examined. The process of dealing with these difficulties is apparently handled by gridding the data, and for that I'll be looking into what McIntyre has found again.
Friday, January 01, 2010
Climate Sciencapades II
I might as well share this shocking discovery that I made this evening.
Shocking to me, at least.
You may recall from my previous post that I came up with a simple-minded way of calculating yearly anomalies, that is by subtracting the mean of all data from a given location from each of the yearly means.
Hansen describes a much more complicated method of calculating the yearly anomalies. I won't go into it at this point, but I was concerned that my simple approach might make a significant difference.
And so I compared the two. That is, anomalies calculated using Hansen's method with my simple method. And here is the result:

The black plot is dset1 with anomalies calculated by Hansen's method. The red dashed plot is dset1 with anomalies calculated using my method. If you have trouble seeing the red plot it's because it's right on top of the black one.
Here's a plot of the difference between the two:
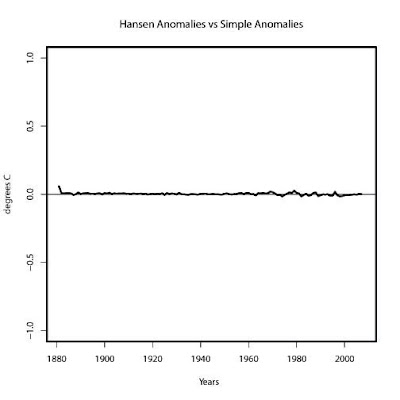
So the difference is very small. Once again Hansen's complicated approach appears to be unnecessary.
Shocking to me, at least.
You may recall from my previous post that I came up with a simple-minded way of calculating yearly anomalies, that is by subtracting the mean of all data from a given location from each of the yearly means.
Hansen describes a much more complicated method of calculating the yearly anomalies. I won't go into it at this point, but I was concerned that my simple approach might make a significant difference.
And so I compared the two. That is, anomalies calculated using Hansen's method with my simple method. And here is the result:

The black plot is dset1 with anomalies calculated by Hansen's method. The red dashed plot is dset1 with anomalies calculated using my method. If you have trouble seeing the red plot it's because it's right on top of the black one.
Here's a plot of the difference between the two:

So the difference is very small. Once again Hansen's complicated approach appears to be unnecessary.
Climate Sciencapades
What is one to do these days with regard to climate change except look at the data oneself? And so I've been doing some of that.
I downloaded raw temperature data sets from http://www.climateaudit.info/data/station/giss, then loaded the files into R:
load("giss.dset0.tab.old") #Data set 0, raw data with some adjustments
load("giss.dset1.tab") #Data set 1, stations at one location combined and adjusted
load("giss.info.tab") #Station data
I was especially interested in the heat island effect as a possible cause of modern land surface warming.
First I compared dset0 and dset1 to get an idea about how adjustments were made:
pt = function(sta, giss.dset0, giss.dset1) {
if(!is.na(giss.dset1[[sta]][1])) {
color = c("red", "green", "blue", "brown", "coral", "darkgreen", "orange", "pink")
par(col="black",lwd=3)
substa = ""
for(i in 1:length(giss.dset0[[sta]])) {
substa = paste(substa, names(giss.dset0[[sta]])[i])
}
plot(giss.dset1[[sta]][[1]][[1]], giss.dset1[[sta]][[1]][[18]],
type="l", main=names(giss.dset1[[sta]]), xlab="Year", ylab="Temp",
sub=substa, xlim=c(1880,2009))
for(i in 1:length(giss.dset0[[sta]])) {
par(col=color[i],lwd = 1)
lines(giss.dset0[[sta]][[i]][[1]], giss.dset0[[sta]][[i]][[18]], lty=i)
}}}
for(sta in 1:length(giss.dset1)) {
pt(sta, giss.dset0, giss.dset1)
print(paste(sta, giss.info[[2]][[sta]], giss.info[[8]][[sta]], sep=" "))
getGraphicsEvent(onKeybd=keybd)
}
With this you can flip through locations and see how dset0 became dset1. One finds some pretty striking adjustments such as segements of data that were left out and stations that were ignored. No doubt the reasons for doing this are good, but it's hard to figure out what the reasons are from the data. For example:

The black plot is the data included in dset1. The colored plots are the raw data from individual stations in the same area that were combined to produce dset1. Note that the data from the third station, from about 1960 to 1985, was not included in dset1. Why? There were a number of examples of this in other locations.
Another example:
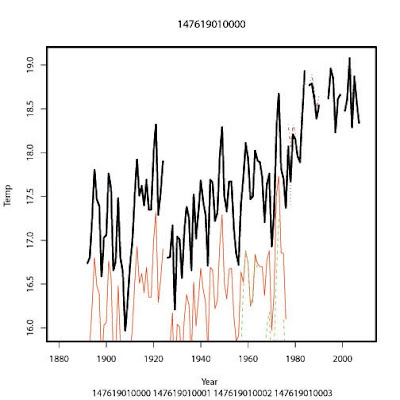
The readings of the two stations in the 1890 to 1975 period were adjusted upward by about 1 degree to produced the dset1 data. What justifies this?
In the final analysis it's the overall effect that's important. We are interested in whether or not the planet itself is getting warmer and by how much. Do these adjustments affect that measurement?
I'm mainly interested in trends, and so I dispensed with gridding of the data. This is valid since we are comparing the same locations with each other in the different sets. My simple minded approach was to average all the data in dset0 by years and compare that to dset1.
#First get mean anomalies for dset0.
#Calculate anomalies as annual mean temps minus the mean of all temps
#for a given location. Throw out locations with less than 30 good
#years.
for(i in 1:length(giss.dset0))
for(j in 1:length(giss.dset0[[i]])) if(is.na(giss.dset0[[i]])[[j]]) next else
{
m = mean(giss.dset0[[i]][[j]]$ANN, na.rm=TRUE)
giss.dset0[[i]][[j]]$anom = giss.dset0[[i]][[j]]$ANN-m
}
years=0; anoms=0
for(i in 1:length(giss.dset0))
for(j in 1:length(giss.dset0[[i]])) if(is.na(giss.dset0[[i]])[[j]]) next else
if(length(giss.dset0[[i]][[j]]$anom)-sum(is.na(giss.dset0[[i]][[j]]$anom)) < 30) next else
{
if(length(years)==1) {
years = giss.dset0[[i]][[j]]$year
anoms = giss.dset0[[i]][[j]]$anom
}
else {
years = c(years, giss.dset0[[i]][[j]]$year)
anoms = c(anoms, giss.dset0[[i]][[j]]$anom)
}
}
dset0.t = data.frame("year"=years, "anom"=anoms)
dset0.means = tapply(dset0.t$anom, dset0.t$year, mean, na.rm=TRUE)
And then to dset1:
#Reorganize the data into a simpler data table and include location info
#for future comparison of rural vs urban stations.
#Put the code in a function for debugging in R.
extr1 = function(giss.dset1, giss.info) {
id = 0; year=0; temp=0; ur = 0; li = length(giss.dset1)
for (i in 1:li) if(sum(is.na(giss.dset1[[i]])) > 0) next else {
for(j in 1:length(giss.dset1[[i]][[1]][[1]])) {
id = c(id, giss.info[[2]][[i]])
ur = c(ur, giss.info[[8]][[i]])
}
year = c(year, giss.dset1[[i]][[1]][[1]])
temp = c(temp, giss.dset1[[i]][[1]][[18]])
}
return(data.frame("id"=id, "ur"=ur, "year"=year, "temp"=temp))
}
dset1.t = extr1(giss.dset1, giss.info)
#Calculate anomaly as annual temp minus mean of all temps
dset1.s = split(dset1.t, dset1.t[[1]])
for(i in 1:length(dset1.s)){
t = mean(dset1.s[[i]][[4]], na.rm=TRUE)
dset1.s[[i]]$anom = dset1.s[[i]]$temp - t
}
dset1.a = unsplit(dset1.s, dset1.t[[1]])
dset1.means = tapply(dset1.means$anom, dset1.means$year, mean, na.rm=TRUE)
#Comparison plot.
par(col="black")
plot(names(dset0.means), dset0.means, type="l", xlab="Year", ylab="degrees C",
main="Data Set1 vs Data Set 0", lwd=3)
abline(coef(line(names(dset0.means), dset0.means)))
par(col="red")
lines(names(dset1.means), dset1.means, lty=2,lwd=3)
abline(coef(line(names(dset1.means), dset1.means)))
And voila!

There is no significant difference between the sets. A very simple averaging of data collected from various stations gives the same plot as an adjusted data set made up of stations painstakingly combined together to represent a given location. At least this is the case where determining anomalies is concerned.
As for the urban effect on temperatures:

This is dset1. The black plot is all of dset1. The red plot is urban locations and the blue plot is rural locations. As you can see there is no difference to speak of in this adjusted data set between urban stations and rural ones. The plots and regression lines all fall on each other for the most part.
The next step in the processing and adjustment of this data is to "grid" it, meaning that an effort is made to determine measurments over the whole surface of the earth in grid squares of a few degrees each. Hansen spends considerable effort making adjustments for urban effects, but it looks like those adjustments are not necessary.
I downloaded raw temperature data sets from http://www.climateaudit.info/data/station/giss, then loaded the files into R:
load("giss.dset0.tab.old") #Data set 0, raw data with some adjustments
load("giss.dset1.tab") #Data set 1, stations at one location combined and adjusted
load("giss.info.tab") #Station data
I was especially interested in the heat island effect as a possible cause of modern land surface warming.
First I compared dset0 and dset1 to get an idea about how adjustments were made:
pt = function(sta, giss.dset0, giss.dset1) {
if(!is.na(giss.dset1[[sta]][1])) {
color = c("red", "green", "blue", "brown", "coral", "darkgreen", "orange", "pink")
par(col="black",lwd=3)
substa = ""
for(i in 1:length(giss.dset0[[sta]])) {
substa = paste(substa, names(giss.dset0[[sta]])[i])
}
plot(giss.dset1[[sta]][[1]][[1]], giss.dset1[[sta]][[1]][[18]],
type="l", main=names(giss.dset1[[sta]]), xlab="Year", ylab="Temp",
sub=substa, xlim=c(1880,2009))
for(i in 1:length(giss.dset0[[sta]])) {
par(col=color[i],lwd = 1)
lines(giss.dset0[[sta]][[i]][[1]], giss.dset0[[sta]][[i]][[18]], lty=i)
}}}
for(sta in 1:length(giss.dset1)) {
pt(sta, giss.dset0, giss.dset1)
print(paste(sta, giss.info[[2]][[sta]], giss.info[[8]][[sta]], sep=" "))
getGraphicsEvent(onKeybd=keybd)
}
With this you can flip through locations and see how dset0 became dset1. One finds some pretty striking adjustments such as segements of data that were left out and stations that were ignored. No doubt the reasons for doing this are good, but it's hard to figure out what the reasons are from the data. For example:

The black plot is the data included in dset1. The colored plots are the raw data from individual stations in the same area that were combined to produce dset1. Note that the data from the third station, from about 1960 to 1985, was not included in dset1. Why? There were a number of examples of this in other locations.
Another example:

The readings of the two stations in the 1890 to 1975 period were adjusted upward by about 1 degree to produced the dset1 data. What justifies this?
In the final analysis it's the overall effect that's important. We are interested in whether or not the planet itself is getting warmer and by how much. Do these adjustments affect that measurement?
I'm mainly interested in trends, and so I dispensed with gridding of the data. This is valid since we are comparing the same locations with each other in the different sets. My simple minded approach was to average all the data in dset0 by years and compare that to dset1.
#First get mean anomalies for dset0.
#Calculate anomalies as annual mean temps minus the mean of all temps
#for a given location. Throw out locations with less than 30 good
#years.
for(i in 1:length(giss.dset0))
for(j in 1:length(giss.dset0[[i]])) if(is.na(giss.dset0[[i]])[[j]]) next else
{
m = mean(giss.dset0[[i]][[j]]$ANN, na.rm=TRUE)
giss.dset0[[i]][[j]]$anom = giss.dset0[[i]][[j]]$ANN-m
}
years=0; anoms=0
for(i in 1:length(giss.dset0))
for(j in 1:length(giss.dset0[[i]])) if(is.na(giss.dset0[[i]])[[j]]) next else
if(length(giss.dset0[[i]][[j]]$anom)-sum(is.na(giss.dset0[[i]][[j]]$anom)) < 30) next else
{
if(length(years)==1) {
years = giss.dset0[[i]][[j]]$year
anoms = giss.dset0[[i]][[j]]$anom
}
else {
years = c(years, giss.dset0[[i]][[j]]$year)
anoms = c(anoms, giss.dset0[[i]][[j]]$anom)
}
}
dset0.t = data.frame("year"=years, "anom"=anoms)
dset0.means = tapply(dset0.t$anom, dset0.t$year, mean, na.rm=TRUE)
And then to dset1:
#Reorganize the data into a simpler data table and include location info
#for future comparison of rural vs urban stations.
#Put the code in a function for debugging in R.
extr1 = function(giss.dset1, giss.info) {
id = 0; year=0; temp=0; ur = 0; li = length(giss.dset1)
for (i in 1:li) if(sum(is.na(giss.dset1[[i]])) > 0) next else {
for(j in 1:length(giss.dset1[[i]][[1]][[1]])) {
id = c(id, giss.info[[2]][[i]])
ur = c(ur, giss.info[[8]][[i]])
}
year = c(year, giss.dset1[[i]][[1]][[1]])
temp = c(temp, giss.dset1[[i]][[1]][[18]])
}
return(data.frame("id"=id, "ur"=ur, "year"=year, "temp"=temp))
}
dset1.t = extr1(giss.dset1, giss.info)
#Calculate anomaly as annual temp minus mean of all temps
dset1.s = split(dset1.t, dset1.t[[1]])
for(i in 1:length(dset1.s)){
t = mean(dset1.s[[i]][[4]], na.rm=TRUE)
dset1.s[[i]]$anom = dset1.s[[i]]$temp - t
}
dset1.a = unsplit(dset1.s, dset1.t[[1]])
dset1.means = tapply(dset1.means$anom, dset1.means$year, mean, na.rm=TRUE)
#Comparison plot.
par(col="black")
plot(names(dset0.means), dset0.means, type="l", xlab="Year", ylab="degrees C",
main="Data Set1 vs Data Set 0", lwd=3)
abline(coef(line(names(dset0.means), dset0.means)))
par(col="red")
lines(names(dset1.means), dset1.means, lty=2,lwd=3)
abline(coef(line(names(dset1.means), dset1.means)))
And voila!

There is no significant difference between the sets. A very simple averaging of data collected from various stations gives the same plot as an adjusted data set made up of stations painstakingly combined together to represent a given location. At least this is the case where determining anomalies is concerned.
As for the urban effect on temperatures:

This is dset1. The black plot is all of dset1. The red plot is urban locations and the blue plot is rural locations. As you can see there is no difference to speak of in this adjusted data set between urban stations and rural ones. The plots and regression lines all fall on each other for the most part.
The next step in the processing and adjustment of this data is to "grid" it, meaning that an effort is made to determine measurments over the whole surface of the earth in grid squares of a few degrees each. Hansen spends considerable effort making adjustments for urban effects, but it looks like those adjustments are not necessary.
Subscribe to:
Posts (Atom)
